Albert Einstein, Our Man of the Century

This month we salute Time magazines man of the century, Albert Einstein, and I will attempt to explain uncle Albert's most important equation. This is the equation that changed the way we look at the universe, and is still the subject of continuing research today. I am speaking of course of the equation
G = 8 * Pi * T
You were expecting perhaps E=mc^2 ? That may be his most famous equation, but it is certainly not his most important, unless you happen to be designing nuclear weapons. No, the G = 8 * Pi * T equation is really the one that changed our view of the universe forever, and in a most dramatic way. To get a handle on what it means and why it is important, we need to go back to the Egyptians, and the building of the pyramids.

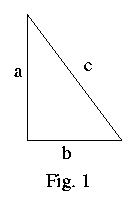
Imagine you were given orders by your pharaoh to build a giant pyramid, and you were given the distinct impression that if it didn't come out right you would be its first occupant. It would be pretty important that the four corners were exactly square, otherwise you would wind up with a lopsided pyramid and an unhappy pharaoh. This brings us to the numbers 3, 4 and 5. Please notice that 3^2 + 4^2 = 9 + 16 = 25 = 5^2, pretty nifty right. This is one instance of a more general principle, called the Pythagorean Theorem, which says that in a right triangle, we always have a^2 + b^2 = c^2 (see fig. 1). Thus to lay out a perfect right angle, get yourself a very long piece of rope, and mark off 12 equal sections. Lay down a segment that is 3 units long, turn left roughly 90 degrees, and lay down a segment that is 4 units long. Now turn left again and head toward the beginning of the rope. Adjust your 90 degree corner (a little) so that when you reach the beginning of the rope your segment contains exactly 5 units, and voila you have just formed a right angle. By making the rope very long, you can make the right angle very exact, and manage to survive the construction project.

What does all of this have to do with Einstein and G = 8 * Pi * T? We are getting there. The important principle at work here is the Pythagorean Theorem, which tells you how to measure distances if you can lay down a grid. To get the distance from A to B, lay down a grid and count how many horizontal and vertical steps you need to take to get from A to B. The distance is then the square root of the sum of the squares. This should sound familiar from high school. Let's apply this rule now to Washington DC, Quito Ecuador, and Singapore. Washington and Quito are at the same longitude, and Quito and Singapore are on the equator, so they form a giant right triangle. Now the airline distances between them are:

Washington DC to Quito Ecuador = 1700 miles
Quito Ecuador to Singapore = 12,255 miles
Singapore to Washington DC = 9660 miles

Yikes! Something is very wrong here. We don't even need to square and add things, we can see that the diagonal of the right triangle is shorter than one of the legs. The problem is that the Pythagorean Theorem is only true on flat surfaces, and as Columbus proved once and for all, the world is not flat. The fact that the sums of the squares for the cities above do not add up is another confirmation of this fact. It also gives us an entry point of finally understanding Einstein's important equation.

You see, the G in Einstein's equation is related to the curvature of space. For many years this has been a mysterious notion for me, and I suspect for you, but I think I've finally got a handle on it. The crux of the question is how can you tell if something is curved. Now its easy if you can stand back far enough, like looking at the earth from the moon, but what if you're living on the planet itself, and there is no external view available? Well, the Pythagorean Theorem again comes to the rescue. You can tell if you are living on a curved surface by making a bunch of measurements like the ones above, and checking to see if the Pythagorean Theorem holds. If it does, then you are living on a flat surface. If a^2 + b^2 > c^2 then you are living on a positively curved surface, like a sphere, while if a^2 + b^2 < c^2 then you are living on a negatively curved surface, like a saddle.

The surface of the Earth is basically two-dimensional (not counting vertical.) You can go north/south or east/west. Einstein's G is actually a set of 16 equations that refer not to a two dimensional surface but a 4 dimensional thingy made up of 3 space dimensions plus time. Don't get confused by this, there is nothing mystical going on, it's just that to write down the true equations of physics, you have to combine space and time together in a certain way. It was another one of Einstein's revolutions that proclaimed that in order to understand the universe, space and time must be considered as one entity, rather than two. His extension of the Pythagorean Theorem was that x^2 + y^2 + z^2 - t^2 = s^2 or that the square of the physical distance minus the square of the time distance equals the spacetime distance, no matter how you observe these events.

We need to understand this a little more clearly before we proceed, and my advice is don't let the presence of time in the equation confuse you. The distance we are measuring is the distance between events, events are things that happen at a certain place and at a certain time. Thus if event A happens at a particular place and time, and event B happens at a nearby place and time, the distance between them is square root of squares of the physical distance minus the square of the time distance. This number will be the same, no matter who does the measuring. Now here is one more wrinkle, if event A and B are connected by a beam of light, then the spacetime distance between them is exactly zero, in other words the space distance equals the time distance. By connected by a beam of light, we mean that event B happens at a place and time that would be reached by a beam of light that was emitted at event A. However, once again, all of this is only true in flat spacetime.

Back to Einstein's G. What G tells you, is how the space and time around you differs from flat spacetime. In other words, it tells you precisely where and when x^2 + y^2 + z^2 - t^2 is different from s^2, and allows you to calculate the difference precisely. This is what curvature looks like in spacetime. Just like on the Earth we could discover curvature by measuring distances and computing the Pythagorean Theorem, in spacetime, we can compute s^2 and discover when it differs from x^2 + y^2 + z^2 - t^2. How? Well, remember the pyramid. As long as the distance was small, the Pythagorean Theorem worked very well, it was only when it took a transcontinental flight that the Earth's curvature started showing up. The same approach works with spacetime, except instead of a two dimensional mesh, we need a three dimensional distance mesh, and a one dimensional time mesh. Once we have created this mesh, (using sticks and clocks), we can compute the distance between nearby events, say the journey the Earth makes a around the sun for a year. Compute the distance every day and add them up, and compare this distance to the total Einstein distance, x^2 + y^2 + z^2 - t^2 where x,y, and z are 0, since we came back to the same location, and t is 1 year, since that's how long it took to come back, and low and behold, you will discover that the two distances don't agree. (Although by a very small factor.) This disagreement shows that there must be some curvature present. This is what is meant by space being curved, it is nothing more than measuring how much spacetime (space squared minus time squared) deviates from flatness, which is where x^2 + y^2 + z^2 - t^2 is always the same, no matter how it is measured.

Now lets take a look at the other half of the equation, namely T. T describes at each point in spacetime (place and time) how much mass, energy, and momentum is present at that place and time. Einstein's equation states that if you know where the mass and energy is, then you can compute the curvature of spacetime that it generates, namely multiply the energy, mass, and momentum, T by 8 Pi, and you get the curvature of space at that point. Back in 1915, this was a revolutionary concept, and its consequences are still being explored today. It was the genius of Einstein who brought us this view of the universe, and forever changed the way we see the world around us.

By the way, as an additional illustration of Einstein's genius, he did not receive a Nobel prize for his work on relativity theory, though he certainly deserved one. No, he had already received a Nobel Prize years earlier, for explaining a completely different aspect of physics, called the photo-electric effect, which was crucial in the development of quantum mechanics. Between these two events, he also created the special theory of relativity, which was also worthy of a Nobel prize all by itself, for it too changed the way we look at world and introduced the original concept of spacetime. One thousand years from now Einstein's contributions to our understanding of the world around us will still be treasured. Not too bad for a college dropout and low ranking civil servant in Switzerland, I'd say.

Sitemap
Go up to How do Things Work Go up to Home Page of Nadine Loves Henry
Go back to Why is the Sky Blue, Daddy Continue with The Green Flash