Starting small
Numbers in the physical world (orders of magnitude)
Number living humans 7 * 10^9 (billions)
Number of stars in the Milky Way 10^11 (100 billions)
US national debt 10^13 (tens of trillions)
Number of ants on the Earth 10^15
Seconds since the big bang 10^17
Starting small
Avogadro's number 10^23
Number of atoms in the universe 10^80
Number of grains of sand to fill the universe 10^90
A google 10^100
Number of protons to fill the universe 10^122
Number of planck volumes to fill the universe 10^185
Now we're getting started
A googleplex
google = 10^100
googleplex = 10 ^ (10 ^ 100)
How long to write down a googleplex?
Greater than the number of quantum states occupied by a human
Knuth up arrow notation
$\displaystyle{\begin{matrix}a\times b&=&\underbrace {a+a+\dots +a} \\&&b{\mbox{ copies of }}\end{matrix}}$
$\displaystyle{\begin{matrix}a\uparrow b=a^{b}=& \underbrace {a\times a\times \dots \times a} \\&b{\mbox{ copies of }}a\end{matrix}}$
$\displaystyle{\begin{matrix}a\uparrow \uparrow b&={\ ^{b}a}=&\underbrace {a^{a^{{}^{.\,^{.\,^{.\,^{a}}}}}}} &= &\underbrace {a\uparrow (a\uparrow (\dots \uparrow a))} \\ &&b{\mbox{ copies of }}a&&b{\mbox{ copies of }}a\end{matrix}}$
What's good once is even better twice
Knuth went on to define a “triple arrow” operator
And a “quadruple arrow” operator

Let's keep going
$\displaystyle{\begin{matrix}N&=a\uparrow \uparrow b&= &\underbrace {a^{a^{{}^{.\,^{.\,^{.\,^{a}}}}}}} \\&&&{\mbox{b copies of a}}\end{matrix}}$$\displaystyle{\begin{matrix}a\uparrow \uparrow \uparrow b&= &\underbrace {a^{a^{{}^{.\,^{.\,^{.\,^{a}}}}}}} \\&&&{\mbox{b-1 towers of N high}}\end{matrix}}$
$a\uparrow ^{n}b$ Things are getting out of hand
Some Numbers
$3\uparrow \uparrow 2=3^{3}=27$
${\displaystyle 3\uparrow \uparrow 3=3^{3^{3}}=3^{27}=7,625,597,484,987}$
$3\uparrow\uparrow 4=3^{3^{3^3}}=3^{3^{27}}=3^{7625597484987}\approx 1.2580143\times 10^{3638334640024}$
$3\uparrow\uparrow 5=3^{3^{3^{3^3}}}=3^{3^{3^{27}}}=3^{3^{7625597484987}}$
From before: ${\displaystyle 3\uparrow \uparrow 3=3^{3^{3}}=3^{27}=7,625,597,484,987}$
Now: ${\displaystyle 3\uparrow \uparrow \uparrow 3 = 3\uparrow \uparrow (3 \uparrow \uparrow 3) = 3\uparrow \uparrow 7,625,597,484,987}$
A tower of 3's 7,625,597,484,987 high
That's a big number, it has about 3.6 trillion digits.
${\displaystyle 3\uparrow \uparrow \uparrow \uparrow 3 = 3\uparrow \uparrow \uparrow (3 \uparrow \uparrow \uparrow 3)}$
A number with a 3.6 trillion digit exponent.
Graham's number
Graham's number is connected to the following problem in Ramsey theory: Connect each pair of geometric vertices of an n-dimensional hypercube to obtain a complete graph on 2n vertices. Colour each of the edges of this graph either red or blue. What is the smallest value of n for which every such colouring contains at least one single-coloured complete subgraph on four coplanar vertices?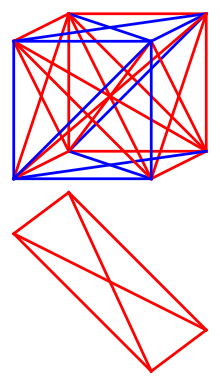
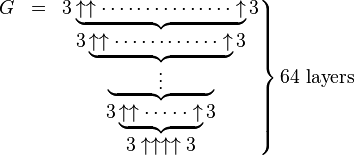
Another big number
Tree(3): https://youtu.be/3P6DWAwwViU

Makes Graham's number look like zero.
Now for a really big number
The Busy Beaver Function
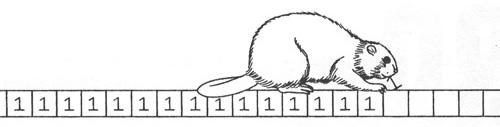
A program is just a set of symbols
100 print 1 200 goto 100This will never halt
A program is just a set of symbols
100 let n = 2 200 n = n + 2 300 print 1 400 if n /= sum of two primes goto 200 500 print "Goldbach conjecture is false"How many ones will this print?
A program is just a set of symbols
Consider all the programs that can be written with N symbols. For
each N, choose the program that writes out the largest number of ones
and halts. This describes a function from N->N.
This is the Busy Beaver Function.
It grows faster than any function we've seen so far.

There are more things in heaven and earth, Horatio, than are dreamt of in your philosophy.